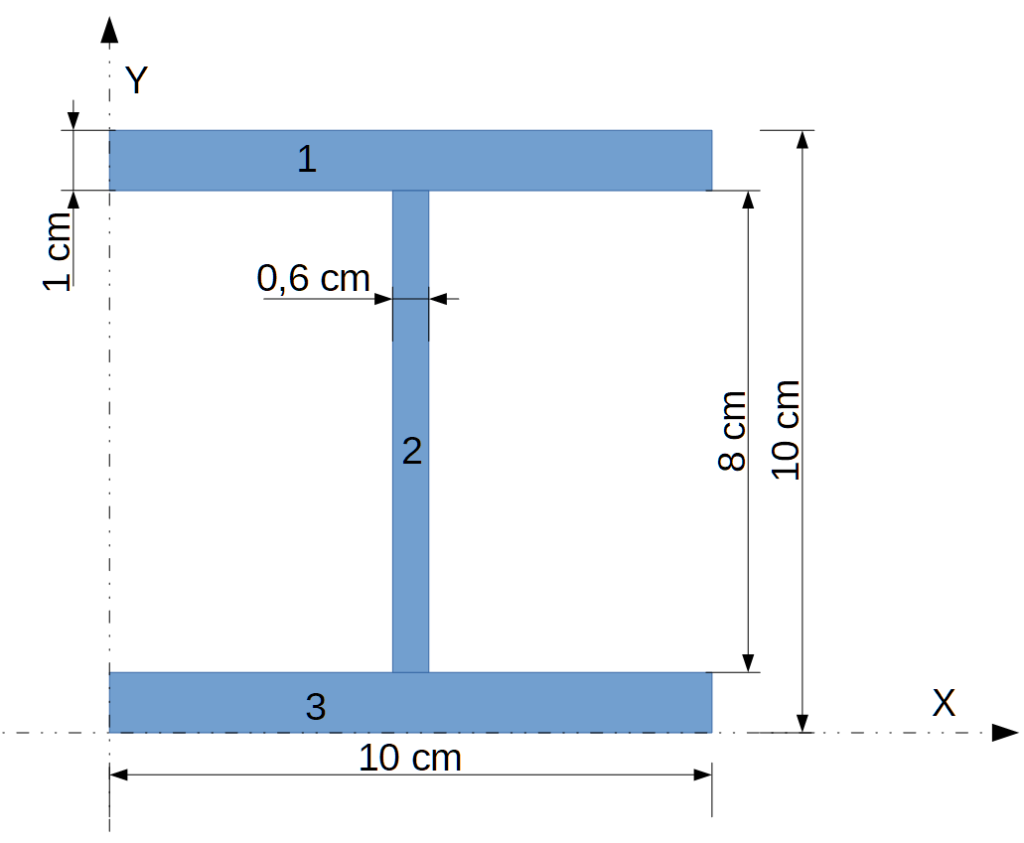
Der Satz von Steiner – Ingenieurbüro Möhn

Um das Flächenträgheitsmoment (sowie die Widerstandsmomente und die Querschnittsfläche) eines beliebigen Profils (orthogonalen Polygons) zu berechnen, teilt man es zweckmäßigerweise in Rechtecke auf. Diese nummeriert man durch und notiert deren Breite, Höhe und Abstand von der Bezugslinie (X-Achse). Auf diese Weise erhält man folgende Tabelle:

n	X	Y	O
1	100	10	90
2	6	80	10
3	100	10	0

Tabelle für ein Profil IPB 100 nach DIN 1025 (alle Angaben in mm).

Außerdem benötigt man noch die Gesamthöhe des Profils, in diesem Fall 100 mm.

Wir berechnen die Schwerelinien der Teilflächen:

e_i={Y_i \over 2}

Wir berechnen den Abstand der Teilflächenschwerelinien von der Grundlinie (Bezugslinie: X-Achse):

ys_i=e_i+O_i

Wir berechnen die Flächeninhalte der Teilflächen:

A_i=X_i\cdot Y_i

Wir berechnen die Gesamtquerschnittsfläche

A_{ges}=\sum_i^n A_i

Wir berechnen das Flächenträgheitsmoment der Teilflächen:

{I_y}_i=A_i \cdot \left( e_i^2 \over 3 \right)

Wir berechnen den Abstand der Gesamtschwerelinie (von unten):

e_u={\sum_i^n \cdot ys_i \over A_{ges}}

Wir berechnen den Abstand der Gesamtschwerelinie (von oben):

e_o=Y_{ges}-e_u

Wir berechnen die Abstände der Teilflächenschwerelinien von der Gesamtschwerelinie:

{\Delta_y}_i=e_u-ys_i

Wir berechnen das Flächenträgheitsmoment des zusammengesetzten Profils:

I_y=\sum_i^n \left( {I_y}_i+A_i \cdot \left( {\Delta^2_y}_i\right)\right)

Wir berechnen das zugseitige Widerstandsmoment:

W_D={I_y \over e_o}

Wir berechnen das druckseitige Widerstandsmoment:

W_D={I_y \over e_u}

Damit sind die statischen Querschnittswerte bestimmt.

Um diese Systematik immer einfach nutzen zu können, schreiben wir ein kurzes Programm.
Dessen (minimaler) Quelltext in Pascal lautet:

program steiner0; 
uses crt; 
var                    i,n:integer; 
        x,y,o,e,ys,a,iy,dy:array[1..9] of real; 
yges,jy,wd,wz,ages,t,eu,eo:real; 
begin clrscr; 
 write('Anzahl Rechtecke= '); 
 readln(n); 
 write('Maximaler Y-Wert= '); 
 readln(yges); 
 for i := 1 to n do 
 begin clrscr; 
  write(i,'. X-Wert eingeben: '); 
  readln(x[i]); 
  write(i,'. Y-Wert eingeben: '); 
  readln(y[i]); 
  write(i,'. 0-Wert eingeben: '); 
  readln(o[i]); 
 end; 
 for i := 1 to n do 
 begin 
   e[i] := y[i]/2; 
  ys[i] := e[i]+o[i]; 
   a[i] := y[i]*x[i]; 
   ages := ages+a[i]; 
  iy[i] := a[i]*((e[i]*e[i])/3); 
      t := t+(a[i]*ys[i]); 
     eu := t/ages; 
     eo := yges-eu; 
 end; 
 for i := 1 to n do 
 begin 
  dy[i] := eu-ys[i]; 
     jy := jy+(iy[i]+a[i]*(dy[i]*dy[i])); 
     wd := jy/eo; 
     wz := jy/eu; 
 end; 
 writeln('Das Moment 2. Grades ist          ',jy:8:3,  ' mm4'); 
 writeln('Widerstandsmoment druckseitig ist ',wd:8:3,  ' mm3'); 
 writeln('Widerstandsmoment zugseitig ist   ',wz:8:3,  ' mm3'); 
 writeln('Der Gesamtquerschnitt ist         ',ages:8:3,' mm2'); 
readkey; 
end.

Beachte!
Bei gewalzten Stahlprofilen liefert das Programm Werte, die weiter auf der sicheren Seite liegen, da ausgerundete Ecken nicht mit einkalkuliert werden.
Bei gekanteten Stahlprofilen weichen die Werte minimal nach unten ab, weil Biegeradien nicht berücksichtigt worden sind.

Das Programm besitzt eine einfach formatierte Ausgabe. Komfortabler ist es, die Ergebnisse in cm zu formatieren:

...,(jy/10000):8:3,' cm4');
...,(wd/1000 ):8:3,' cm3');
...,(wz/1000 ):8:3,' cm3');
...,(ages/100):8:3,' cm2');

Zur Kontrolle:
Bei richtiger Ausführung der Berechnung lautet das Ergebnis für das oben dargestellte Profil IPB 100

Flächenträgheitsmoment= 432{,}2 \mathbf {~cm^4} \\ Widerstandsmoment=86{,}45 \mathbf {~cm^3} \\ Querschnittsfläche= 24{,}80 \mathbf {~cm^2}

Hinweis:
Die DIN nennt die realen Werte (mit Walzradien)

I_y=450 \mathbf {~cm^4} \\ W_y=89{,}8 \mathbf {~cm^3}\\ A_{ges}=26{,}0 \mathbf {~cm^2}

Stabilitätsnachweise, die mit dem gelisteten Programm berechnet wurden, liegen mithin auf der sicheren Seite.